How Many Elements In The Quotient Ring

Quotient rings and homomorphisms.

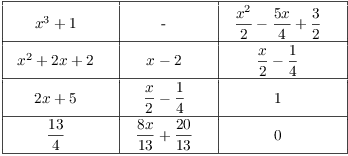
How many elements in the quotient ring. Need a work around. C compute express your answer in the form where. Theorem 6 5 gives the fact that addition and multiplication are well de ned on congru ence classes. X 2 1 which is the defining property of i.

A if x is an element of a ring r the ideal hxi consists of all multiples of x by elements of r. Translating this into the language of cosets gives theorem 6 8. Rep a representative of the element in r. Polynomial ring instance check.

The quotient ring r x x 2 1 is naturally isomorphic to the field of complex numbers c with the class x playing the role of the imaginary unit i. Sage structure element ringelement an element of a quotient ring r i. Let i be an ideal in a ring r ifa i b iand c i d i in r i then a c i b d iand ac i bd i. Finding integer solutions to systems of polynomial equations.

Parent the ring r i. Let be a commutative ring and let be the set of elements which are not zero divisors in. A has no roots in. Let rand sbe rings.

Just take and form the quotient ring where is an irreducible polynomial of degree n. We prove that the quotient ring f 3 x x 2 1 is a field of order 9. B is the quotient ring z4 z6 h 2 2 i an integral domain. The quotient ring r iis the set of distinct additive cosets a i with addition and multipli cation dened by a i b i a b iand a i b i ab i.

Cokernel of a map between modules over polynomial rings. A list the elements of the cosets of h 2 2 i in the ring z4 z6. If is a domain then and the total quotient ring is the same as the field of fractions. We also find the inverse element of each nonzero element ax b in the field.

Model of polynomial with integer coefficients. Since is a cubic it follows that it s irreducible. The reason is that we forced x 2 1 0 i e. Class sage rings quotient ring element quotientringelement parent rep reduce true.

This justifies the notation which is sometimes used for the field of. Then is a multiplicatively closed set hence we may localize the ring at the set to obtain the total quotient ring. Exponent overflow in polynomialring. Computations in a quotient ring a show that is a field.